More on Plotting

This article demonstrates how users can experiment with the plotting options to enhance the reporting of their results.

For illustration, we utilize the same Motivating Example as in the short tutorial. The only distinction is that we employ several denoising strategies here.

## Generate data.
set.seed(1986)

n <- 500
k <- 1

X <- matrix(runif(n * k), ncol = k)
colnames(X) <- paste0("x", seq_len(k))
D <- rbinom(n, size = 1, prob = 0.5)
mu0 <- X[, 1]
mu1 <- X[, 1]
Y <- mu0 + D * (mu1 - mu0) + rnorm(n, sd = sqrt(5))

## Sample split.
train_idx <- sample(c(TRUE, FALSE), length(Y), replace = TRUE)

X_tr <- matrix(X[train_idx, ])
X_val <- matrix(X[!train_idx, ])

D_tr <- D[train_idx]
D_val <- D[!train_idx]

Y_tr <- Y[train_idx]
Y_val <- Y[!train_idx]

## CATEs estimation.
# T-learner.
forest_treated <- regression_forest(as.matrix(X_tr[D_tr == 1, ]), Y_tr[D_tr == 1])
forest_control <- regression_forest(as.matrix(X_tr[D_tr == 0, ]), Y_tr[D_tr == 0])
cates_val_t <- predict(forest_treated, X_val)$predictions - predict(forest_control, X_val)$predictions 

# Causal forest.
forest <- causal_forest(X_tr, Y_tr, D_tr) 
cates_val_cf <- predict(forest, X_val)$predictions 

## Define arguments.
cates_val <- list("T-learner" = cates_val_t,
                  "CF" = cates_val_cf)

strategies <- c("WR", "HT")
denoising <- c("none", "cddf2", "mck1")

pscore_val <- rep(0.5, length(Y_val)) # True propensity scores.

## Call main function.
validation <- valiCATE(Y_tr, Y_val, D_tr, D_val, X_tr, X_val, cates_val, strategies = strategies, denoising = denoising, pscore_val = pscore_val, verbose = FALSE)

GATES

As explained in the short tutorial, we can call the plot method and set the target argument to GATES to display GATES point estimates and 95% confidence intervals. However, due to the relatively large number of models we estimated above, the results may be difficult to interpret.

## GATES plot - default.
plot(validation, target = "GATES")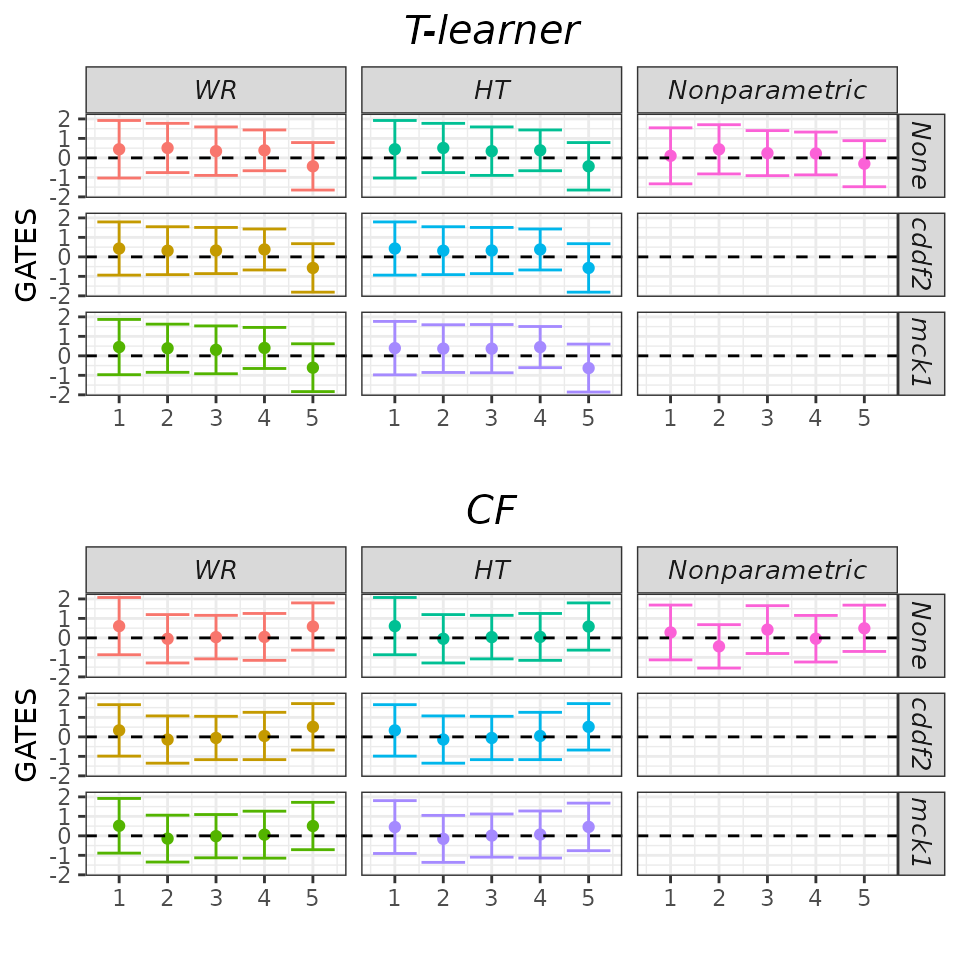

Fortunately, the results are quite robust across models. Therefore, it’s reasonable to display only a subset of them and possibly relegate the remaining ones to an appendix. We can achieve this by using the which_models argument. Here, we choose to display only those models that do not utilize any denoising strategy.

## GATES plot - Subset models.
plot(validation, target = "GATES", 
     which_models = c("wr_none", "ht_none", "imai_li"))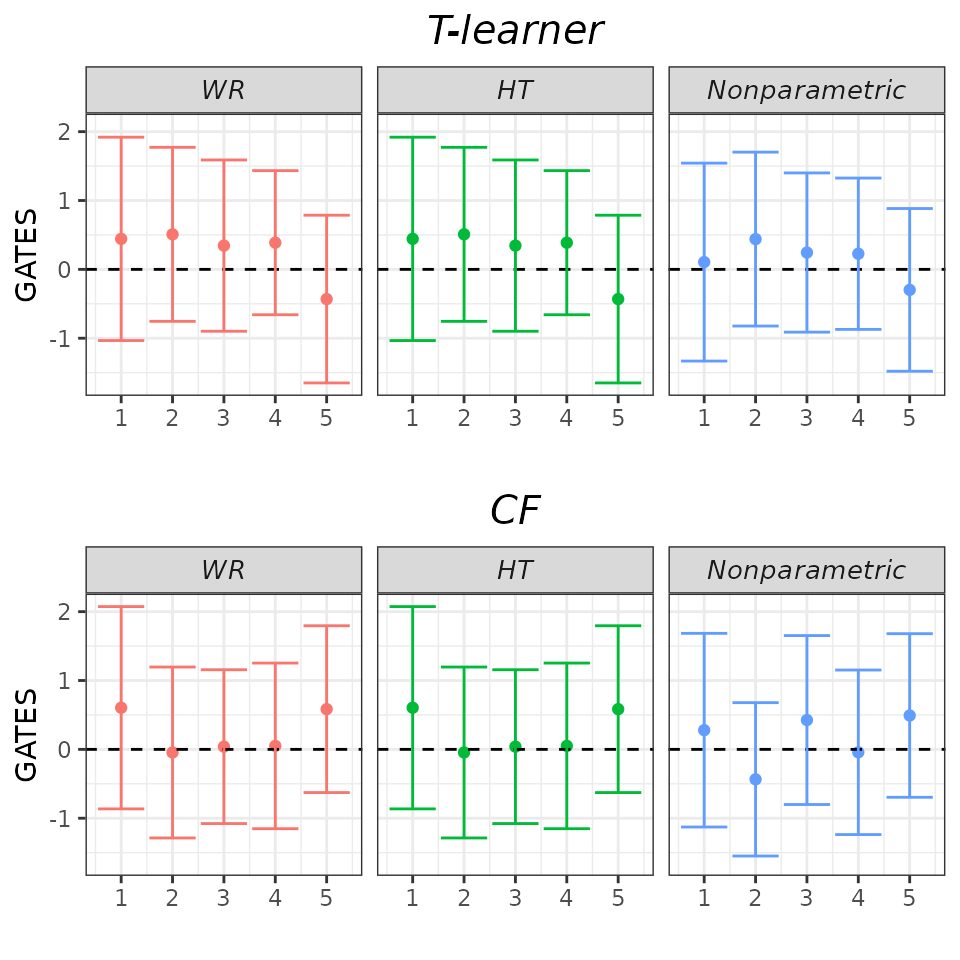

Finally, we can set the gates_hline argument to FALSE to omit the horizontal dashed line. While we may not necessarily need this option here, it’s useful to know that it’s available.

## GATES plot - drop zero line.
plot(validation, target = "GATES", 
     which_models = c("wr_none", "ht_none", "imai_li"), 
     gates_hline = FALSE)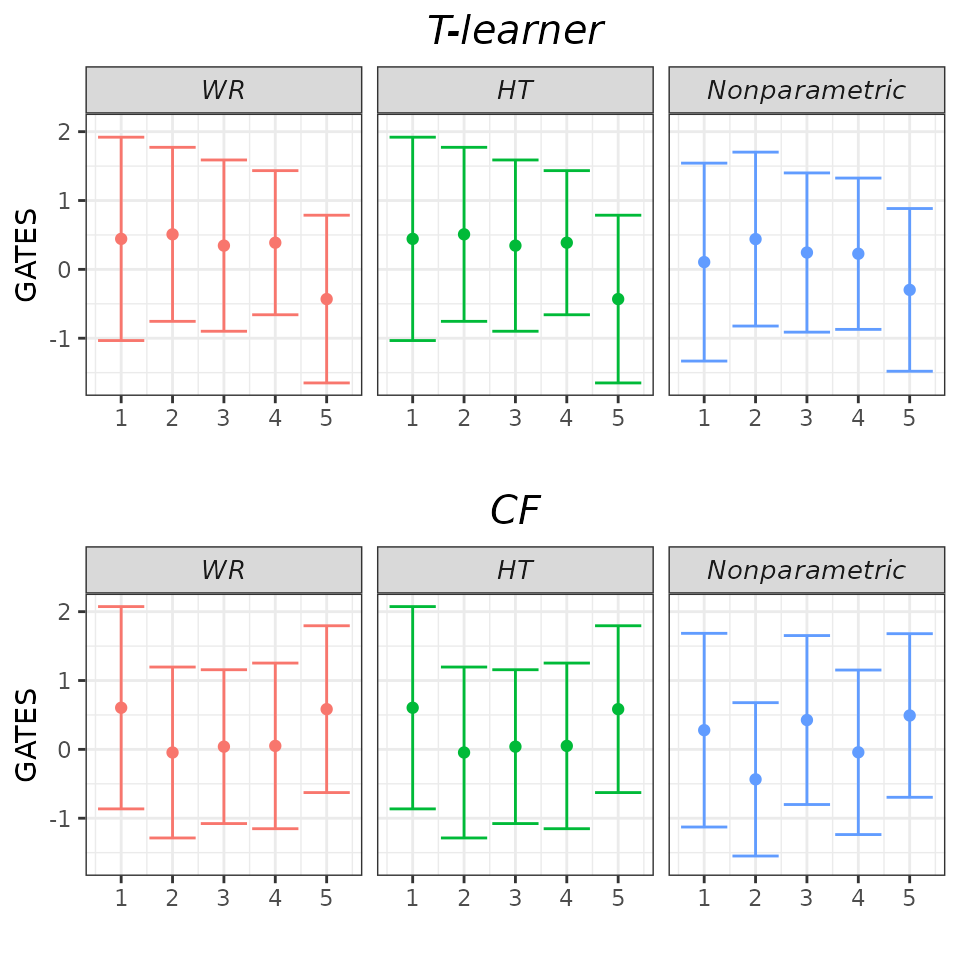

RATEs

As explained in the short tutorial, we can plot the estimated TOC curve by calling the plot method and setting the target argument to TOC. However, the displayed curve can be quite jumpy, especially for low fractions of treated units where the variance of estimation is larger.

## TOC plot - default.
plot(validation, target = "TOC")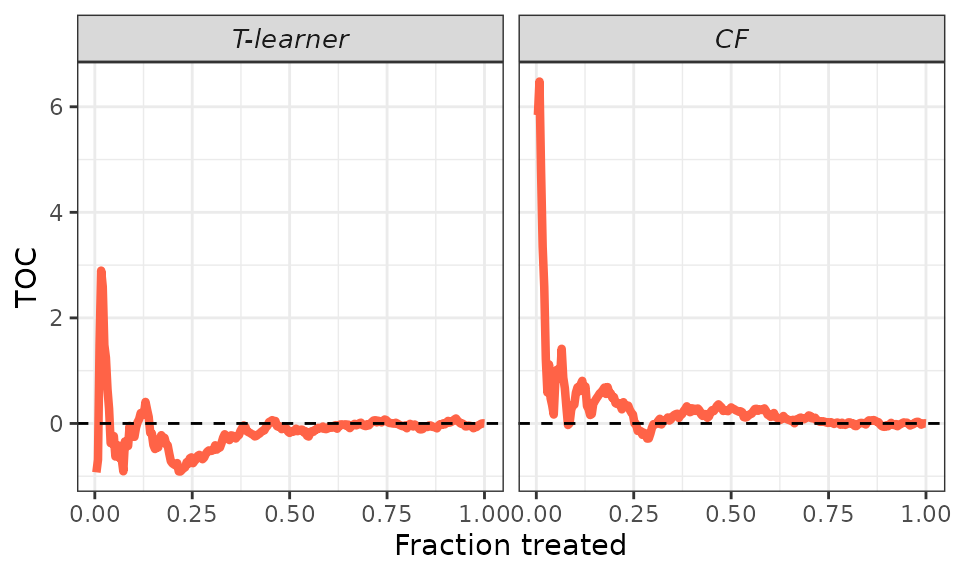

We can smooth the curve by adjusting the toc_smoother argument. Smoothing is accomplished by displaying the TOC for a subset of units in the validation sample. Specifically, if toc_smoother equals 2, we display the TOC of every other unit; if toc_smoother equals 3, we display the TOC of every third unit, and so forth.

## TOC plot.
# Smooth.
plot(validation, target = "TOC", 
     toc_smoother = 5)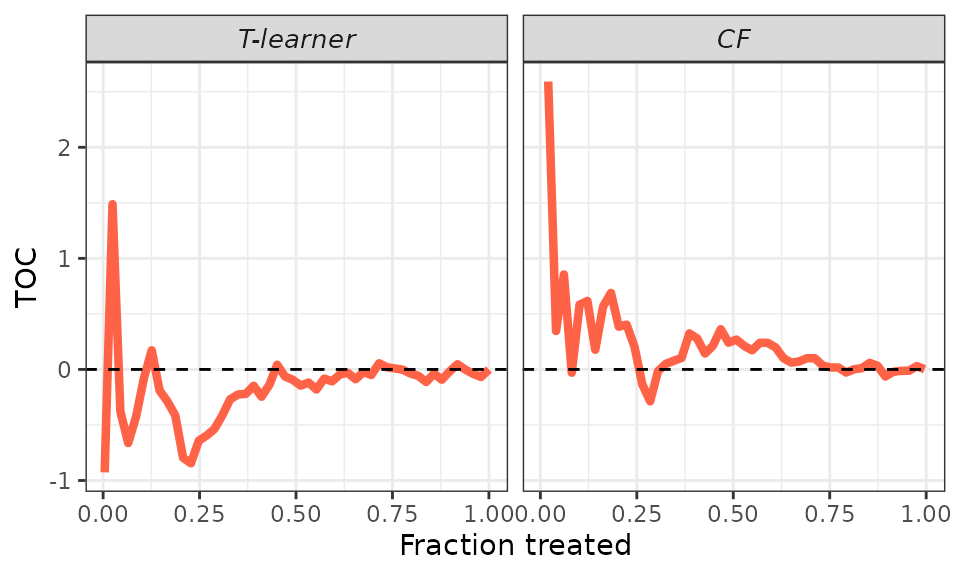

# Smoother.
plot(validation, target = "TOC", 
     toc_smoother = 10)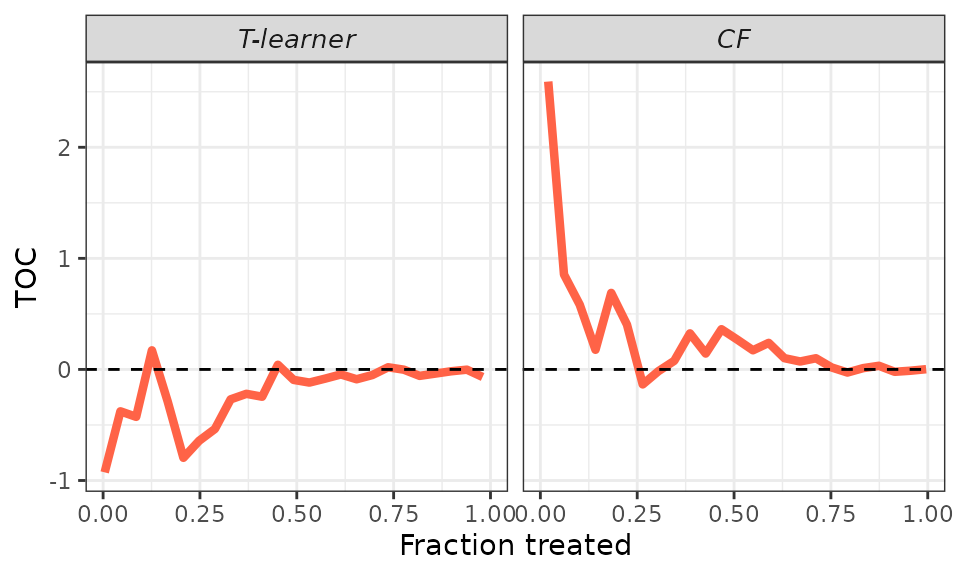

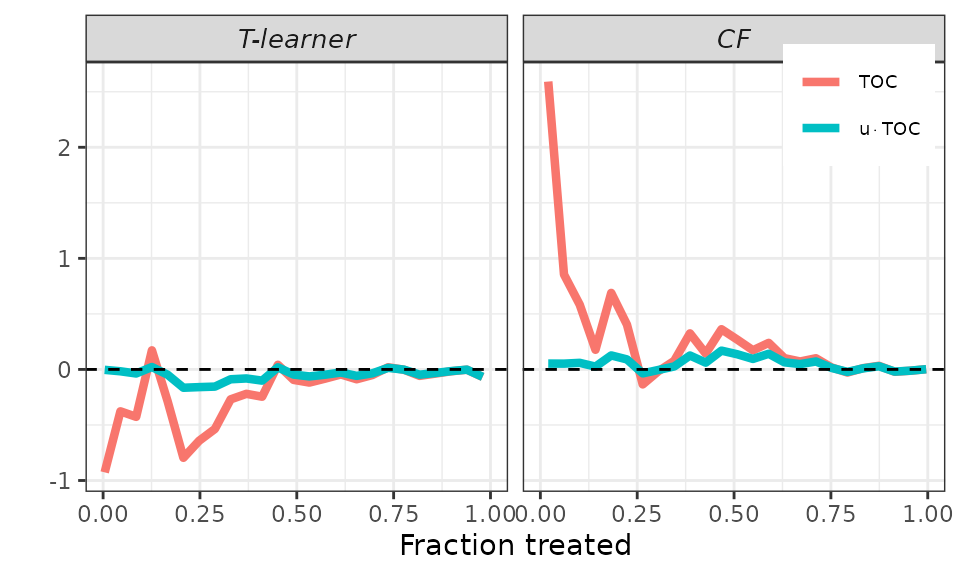
Finally, remember that the AUTOC coefficient corresponds to the area under the TOC curve, while the QINI coefficient corresponds to the area under the curve $u \times TOC (u; \hat{\tau})$. To facilitate an immediate graphical comparison of the two coefficients, it makes sense to plot both the TOC curve and the new curve together. This is accomplished using the plot method and setting the target argument to RATE. It’s worth noting that we can still use the toc_smoother argument to smooth the curves.

## RATEs plot.
# Default.
plot(validation, target = "RATE")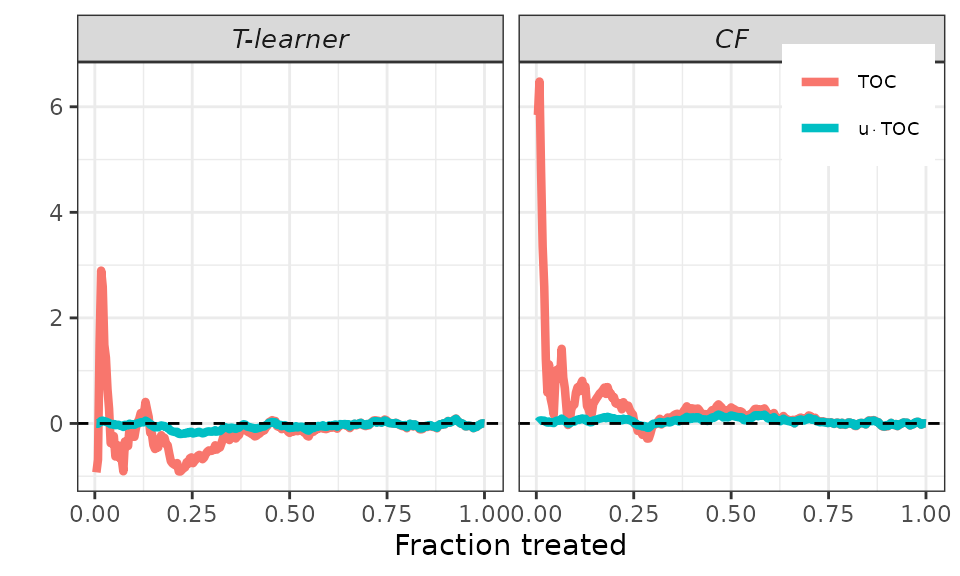

# Smooth.
plot(validation, target = "RATE", 
     toc_smoother = 5)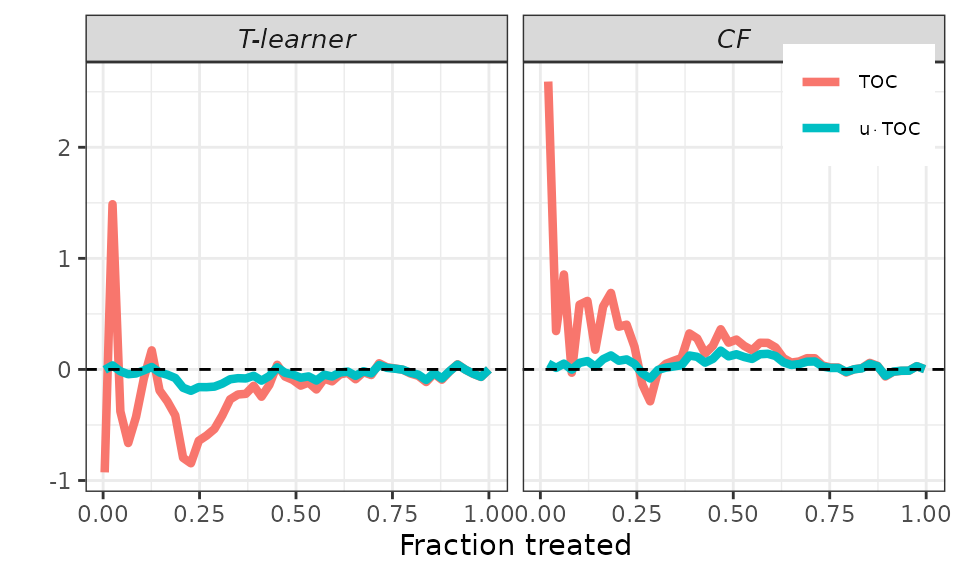

# Smoother.
plot(validation, target = "RATE", 
     toc_smoother = 10)