Causal Inference for Qualitative Outcomes under Instrumental Variables

Causal Inference for Qualitative Outcomes under Instrumental Variables

causalQual_iv(Y, D, Z)

Arguments

Y

Qualitative outcome before treatment. Must be labeled as \(\{1, 2, \dots\}\).

D

Binary treatment indicator.

Z

Binary instrument.

Value

An object of class causalQual.

Details

Under an instrumental-variables design, identification requires the instrument to be independent of potential outcomes and potential treatments (exogeneity), that the instrument influences the outcome solely through its effect on treatment (exclusion restriction), that the instrument has a nonzero effect on treatment probability (relevance), and that the instrument can only increase/decrease the treatment probability (monotonicity). If these assumptions hold, we can recover the local probabilities of shift for all classes:

$$\delta_{m, L} := P(Y_i(1) = m | i \, is \, complier) - P(Y_i(0) = m | i \, is \, complier), \, m = 1, \dots, M.$$

causalQual_iv applies, for each class m, the standard two-stage least squares method to the binary variable \(1(Y_i = m)\). Specifically, the routine first estimates the following first-stage regression model via OLS:

$$D_i = \gamma_0 + \gamma_1 Z_i + \nu_i,$$

and constructs the predicted values \(\hat{D}_i\). It then uses these predicted values in the second-stage regressions:

$$1(Y_i = m) = \alpha_{m0} + \alpha_{m1} \hat{D}_i + \epsilon_{mi}, \quad m = 1, \dots, M.$$

The OLS estimate \(\hat{\alpha}_{m1}\) of \(\alpha_{m1}\) is then our estimate of \(\delta_{m, L}\). Standard errors are computed using conventional procedures and used to construct conventional confidence intervals. All of this is done by calling the ivreg function.

References

• Di Francesco, R., and Mellace, G. (2025). Causal Inference for Qualitative Outcomes. arXiv preprint arXiv:2502.11691. doi:10.48550/arXiv.2502.11691 .

See also

causalQual_soo causalQual_rd causalQual_did

Author

Riccardo Di Francesco

Examples

## Generate synthetic data.
set.seed(1986)

data <- generate_qualitative_data_iv(100, outcome_type = "ordered")

Y <- data$Y
D <- data$D
Z <- data$Z

## Estimate local probabilities of shift.
fit <- causalQual_iv(Y, D, Z)

summary(fit)
#> 
#> ── CAUSAL INFERENCE FOR QUALITATIVE OUTCOMES ───────────────────────────────────
#> 
#> ── Research design ──
#> 
#> Identification:          Instrumental Variables 
#> Estimand:                Local Probability Shifts 
#> Outcome type:            
#> Classes:                 1 2 3 
#> N. units:                100 
#> Fraction treated units:  0.53 
#> 
#> 
#> ── Point estimates and 95\% confidence intervals ──
#> 
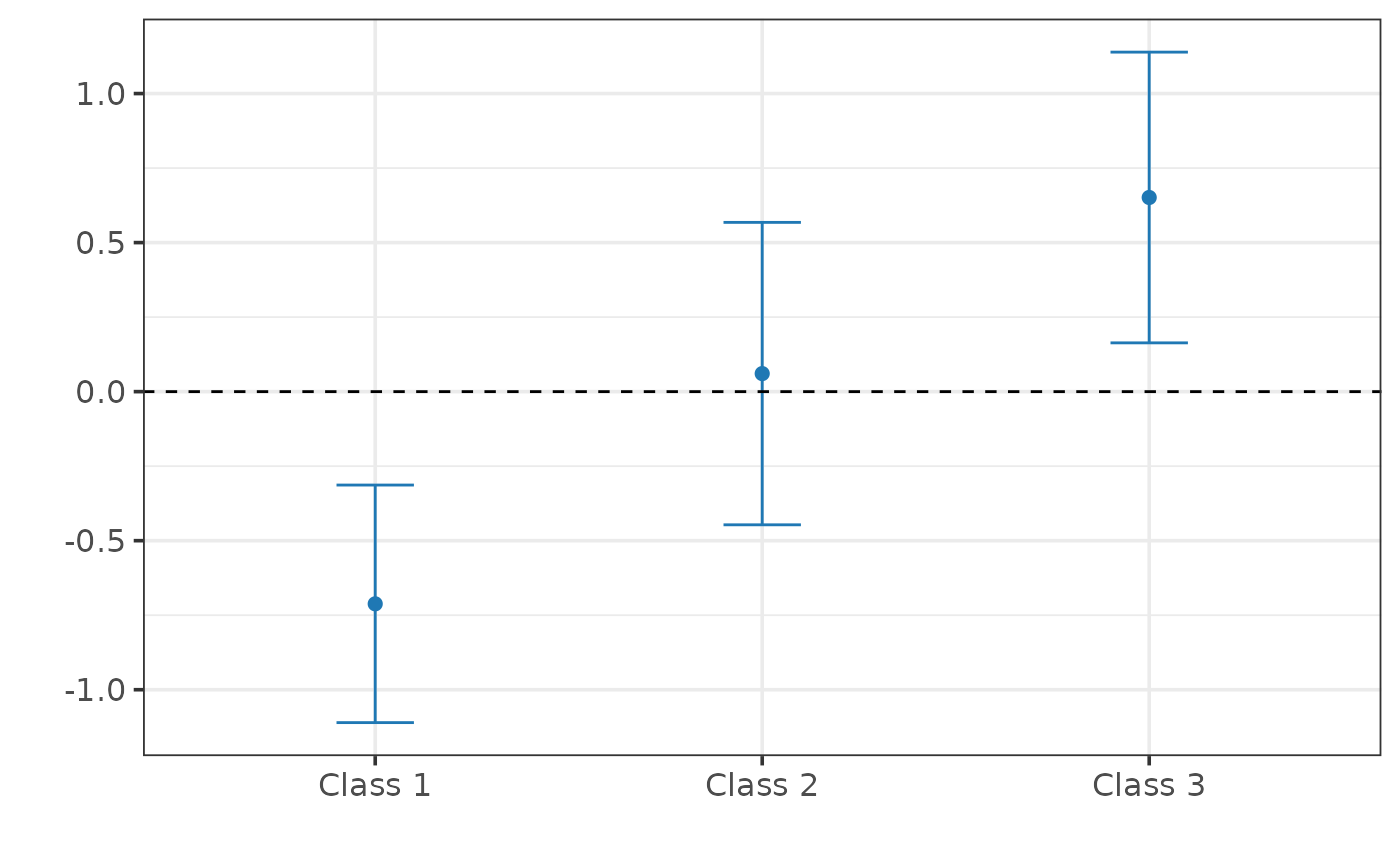
#> Class 1: -0.712  [-1.110, -0.313]
#> Class 2:  0.061  [-0.447,  0.568]
#> Class 3:  0.651  [ 0.164,  1.139]
plot(fit)